Zinsen auf Zinserträge bezeichnet man als Zinseszins. Bei periodischer Wiederanlage ergibt sich der Anlagebetrag aus einer wiederholten Anwendung der Formel für die einfache Verzinsung. Wenn beispielsweise bei einem Anlagezeitraum von zwei Jahren Zinsen nach Ablauf des ersten Jahres gutgeschrieben und erneut angelegt werden, gilt folgender Zusammenhang:
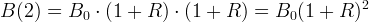 |
(2) |
Nach zwei Jahren und einem jährlichen Zinssatz R wächst der Anfangsbetrag B0 also auf B(2) an. Bei jährlicher Wiederanlage für einen beliebigen Zeitraum von N Jahren gilt:
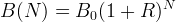 |
(3) |
Beispiel: es werden 1000 Euro über 10 Jahre zu einem Zinssatz von 4% mit jährlicher Wiederanlage von Zinserträgen investiert. Nach 10 Jahren wächst dieser Betrag auf 1480.24 Euro an.
-
B(10) = 1000 * (1.04)∧10 = 1000 * 1.48024 = 1480.24
Auf handelsüblichen Taschenrechnern findet sich zum Potenzieren meist eine Taste „y∧x“. Wenn Sie also „1.04 y∧x 10“ eingeben, sollte das Ergebnis 1.48024 erscheinen. Wenn Zinsen mehrmals jährlich gutgeschrieben und wieder angelegt werden, gilt eine Erweiterung der Formel (3). Die Zahl der jährlichen Wiederanlagezyklen ist m, und nach N Jahren wächst der Anfangsbetrag auf
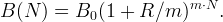 |
(4) |
Die Zahl der Wiederanlagezyklen nennt man auch Wiederanlagefrequenz. Beispiel: es werden 1000 Euro über 10 Jahre zu einem Zinssatz von 4% mit halbjährlicher Wiederanlage investiert. Nach 10 Jahren ergeben sich 1485.95 Euro.
-
B(10) = 1000 * (1 + 0.04 / 2)∧(2 * 10) = 1000 * 1.485947 = 1485.95
In der nachfolgenden Tabelle sind Ergebnisse für ausgewählte Wiederanlagefrequenzen zusammengefasst, die Wiederanlagefrequenz „0“ enspricht der einfachen Verzinsung. Bei jährlicher Wiederverzinsung resultiert gegenüber der einfachen Verzinsung immerhin ein Mehrbetrag von 80,24 Euro. Je häufiger jedoch die Wiederverzinsung, desto bescheidener fällt der Effekt einer weiteren Erhöhung aus, denn mit dem Sprung von monatlicher zu täglicher Wiederanlage ist nur noch ein Zugewinn von 96 Cents verbunden. Es liegt also die Vermutung nahe, dass der Endbetrag bei beliebig hoher Wiederanlagefrequenz nicht über alle Grenzen wächst, sondern einem endlichen Betrag entgegen strebt. Mit der Herleitung der kontinuierlichen Wiederanlage im Abschnitt 5 wird diese Vermutung bestätigt.
| Wiederanlagefrequenz | Endbetrag € |
| 0 | 1400,00 |
| 1 | 1480,24 |
| 2 | 1485,95 |
| 4 | 1488,86 |
| 12 | 1490,83 |
| 365 | 1491,79 |