Monte-Carlo-Simulation ist ein einfaches Mittel zur Abschätzung von Renditen komplexer Anlageinstrumente. Dies wird anhand des Beispiels des Erwartungswerts, der Rendite und der Varianz der geometrischen Brownschen Molekularbewegung (GBM) demonstriert.
Aufgrund seiner Ähnlichkeit mit Finanzzeitreihen ist GBM eine Grundlage gebräuchlicher Preismodelle für Derivate, wie z. B. der Black-Scholes-Formel für Optionen. Ein wichtiges Merkmal von GBM ist eine von der deterministischen Wachstumsrate abweichende Rendite. Um jedoch ein mathematisches Verständnis dieser lognormalen Eigenschaften zu erlangen, ist stochastischer Calculus erforderlich. Hier bietet sich Monte-Carlo-Simulation als einfache Alternative an, Werte auf empirische Weise zu schätzen, welche selbst dann funktioniert, wenn keine analytischen Modelle existieren.
GBM in diskreten Zeitschritten
Im konkreten Experiment werden Szenarien aus der Differentialgleichung für GBM in diskreten Zeitschritten generiert.
\begin{align}
\Delta S_t &= r S_t \Delta t + \sigma S_t \sqrt{\Delta t} ~\epsilon_t
\end{align}\begin{aligned}
S_t &: \mathrm{Wert~zum~Zeitpunkt}~t\\
r &: \mathrm{Wachstumsrate}\\
\sigma &: \mathrm{Volatilität}\\
\Delta t &: \mathrm{Diskrete~Zeitschritte}\\
\epsilon_t &\overset{\mathrm{iid}}{\sim} N(0,1)
\end{aligned}Der Simulationsalgorithmus muss also eine kleine, aber im Wesentlichen willkürliche Zeitspanne Δt sowie einen Startwert S0 zum Zeitpunkt Null auswählen und unabhängige, normalverteilte (iid) Schocks ϵt aus einem Zufallszahlengenerator ziehen. GBM-Pfade entstehen dann durch Akkumulieren einer großen Anzahl von ΔSt in rekursiven Anwendungen von Gleichung (2):
\begin{align}S_{t+1} = S_{t} + \Delta S_t
\end{align}Die Simulation soll verifizieren, dass sich die erwartete Rendite R tatsächlich von der Wachstumsrate r unterscheidet. Außerdem wird die GBM-Varianz geschätzt. Theoretisch sollten diese Werte wie folgt sein:
\begin{aligned}
E[S_t] &= S_0~e^{rt}\\
E[R] &= r - \frac{\sigma^2}{2}\\
Var[S_t] &= S_0^2~e^{2rt}(e^{\sigma^2t}-1)
\end{aligned}Monte-Carlo-Simulations-Experiment und Formeln
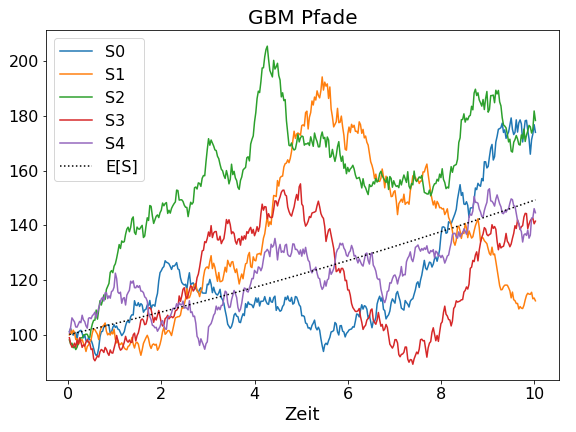
Die Eigenschaften von GBM sollen nun in einem Experiment mit 10.000 Monte-Carlo-Pfaden abgeschätzt werden. Abbildung 1 zeigt fünf solcher Beispiel-GBM-Pfade mit dem erwarteten Pfadwert als gepunkteter Linie. Simulationsparameter für Gleichung (1) sind r = 4 %, σ = 10 %, Δt = 7 Tage und S0 = 100 als Startwert für die Rekursion. Darüber hinaus beträgt die Simulationszeitspanne 10 Jahre, was insgesamt 522 Datenpunkte pro Pfad ergibt. Die gesuchten GBM-Charakteristika können nun mit folgenden Formeln berechnet werden:
\begin{align}
\bar{S_t} &= \frac{1}{N}\sum_{i=0}^{N}{S_{ti}}\\
Var[S_t] &= \frac{\sum_{i=0}^{N}{(S_{ti}-\bar{S_t})^2}}{N-1}\\
Var[\bar{S_t}] &= \frac{1}{N}Var[S_t]\\
R_{ti} &= \frac{1}{t}log(\frac{S_{ti}}{S_0})\\
\bar{R_t} &= \frac{1}{N}\sum_{i=0}^{N}{R_{ti}}\\
Var[R_t] &= \frac{\sum_{i=0}^{N}{(R_{ti}-\bar{R_t})^2}}{N-1}\\
Var[\bar{R_t}] &= \frac{1}{N}Var[R_t]\\
\end{align}\begin{alignat*}{2}
\bar{S_t} &&~:~ &\mathrm{Mittelwert ~ der ~ Pfade}\\
R_{ti}&& ~:~ &\mathrm{Rendite~zu ~Pfad}~i\\
\bar{R_t} &&~:~&\mathrm{Mittelwert~der~Rendite}\\
i &&~:~&\mathrm{Scenario~Index}\\
\end{alignat*}In den Gleichungen (5) und (9) sind, als Folge des zentralen Grenzwertsatzes[1], die Varianzen des Mittelwerts kleiner als die Gesamtvarianzen. Dieser Präzisionsgewinn ist natürlich der springende Punkt, weshalb Monte-Carlo-Simulationen mit einer hohen Anzahl von Szenarien durchgeführt werden. Die Mittelwerte aus den Gleichungen (3) und (7) dienen dann als konsistente Schätzer für den erwarteten Pfadwert und die Anlagerendite.
\begin{align}
\widehat{E[S_t]} &= \bar{S_t}\\
\widehat{E[R_t]} &= \bar{R_t}
\end{align}Jedoch kann die deterministische Wachstumsrate nicht direkt geschätzt werden, sondern ergibt sich aus der Umschreibung der Gleichung für E[St] in Bezug auf die Wachstumsrate r:
\begin{aligned}
\widehat{E[S_t]} &= S_0~e^{\hat{r} t}\\
\Leftrightarrow\hat{r} &=\frac{1}{t}ln(\frac{\widehat{E[S_t]}}{S_0})
\end{aligned}Ergebnisse der Simulation zur geometrischen Brownschen Molekularbewegung
Die Monte-Carlo-Simulation liefert die folgenden Schätzwerte für die GBM-Pfade des Experiments:
| Eigenschaft | Wert | 95% KI |
|---|---|---|
| E[St] | 149,33 | 148,38 – 150,29 |
| r | 4,0082% | 3,9442 – 4,0719% |
| Var[St] | 2368,7 | N/A |
| E[Rt] | 3,5037% | 3,4414 – 3,5659% |
Die Schätzung der aus E[St] errechneten Wachstumsrate r liegt nahe am Eingangs- und theoretischen Wert von 4 %. Darüber hinaus liegt die Schätzung für die erwartete Anlagerendite E[Rt] etwa 0,5 % unter der Wachstumsrate. Mit einem Wert von σ = 10 % entsprechend σ2/2 = 0,5 %werden die theoretischen Vorhersagen auch hier bestätigt. Daraus folgt eine sehr wichtige und nützliche Erkenntnis für Anlagestrategien aller Art: Volatilität ist schlecht für die Rendite!
Zum Schluß noch zur Varianz: mit r=4%, S0=100, σ=10% und t=10 ergibt sich ein theoretischer Wert von 2340,62. Das ist wiederum recht nah an der Schätzung von 2368,7. Monte-Carlo-Simulation funktioniert!
Referenzen
[1] Central Limit Theorem: Wikipedia.org