Annuitäten definieren Serien periodisch wiederkehrender Zahlungen, deren Gesamtwert mit Berechnungsformeln ermittelt werden kann. Die nachfolgend vorgestellten Formeln gelten für Serien gleichhoher Zahlungen in gleichbleibenden zeitlichen Abständen mit gleichbleibender Verzinsung. Der Gegenwartswert fällt auf den Beginn der ersten Periode und der Zukunftswert auf das Ende der letzten Periode. Für gewöhnliche Annuitäten, bei denen die regelmäßigen Zahlungen C jeweils am Periodenende erfolgen, gilt:
| C : | Periodische Zahlung |
| i : | Periodenzins |
| r : | Jahreszins |
| m : | Perioden pro Jahr |
| N : | Zahl der Perioden |
| GW : | Gegenwartswert |
| ZW : | Zukunftswert |
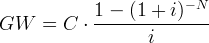 |
(1) |
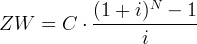 |
(2) |
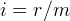 |
(3) |
Bei vorschüssigen Annuitäten fallen die regelmäßigen Zahlungen jeweils an den Periodenanfang. Die modifizierten Berechnungsformeln für den vorschüssigen Gegenwartswert GWv und Zukunftswert ZWv lauten:
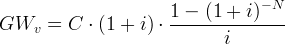 |
(4) |
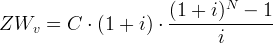 |
(5) |
2.1 Anwendungsbeispiele
2.1.1 Ratenkredit mit vollständiger Tilgung
Beispiel 1: ein Ratenkredit wird in 24 Monatsraten zu 100€ bei einem Zinssatz von 3% vollständig getilgt. Wie hoch ist die zum Vertragsbeginn ausgezahlte Kreditsumme? Lösung: die Kreditsumme ist der Gegenwartswert der 24 Monatsraten und wird mit Formel (1) berechnet. Da es sich um Monatsraten handelt ist der Periodenzins
-
i = r / m = 3% / 12 = 0.25%.
Damit ergibt sich für die Kreditsumme:
-
GW = 100 * (1 – (1 + 0.25 / 100)∧(-24)) / 0.25 * 100 = 2326.60
Beispiel 2: ein Ratenkredit von 1000€ wird in 36 Monatsraten bei einem Zinssatz von 3% vollständig getilgt. Wie hoch sind die Monatsraten? Lösung: hierzu muss Formel (1) für die Ratenzahlung aufgelöst werden. Die Monatsrate beträgt:
-
C = 1000 * 0.25 / 100 / (1 – (1 + 0.25 / 100)∧(-36)) = 29.08
2.1.2 Ratenkredit mit teilweiser Tilgung
Ratenkredite mit teilweiser Tilgung können aus einer Kombination der Zinseszinsformel und Formel (2) berechnet werden.
Beispiel 1: 5000€ aus einem Baukredit über 25000€ sollen in 60 Monatsraten getilgt werden. Der Zinssatz beträgt 4%. Lösung: nach 60 Monaten entsprechend 5 Jahren müssen sich die Verbindlichkeiten auf 20000€ reduzieren. Ohne Ratenzahlungen (Zinsen + Tilgung) wüchse die Kreditsumme KS gemäß der Zinseszinsformel bei monatlicher Wiederanlage auf 30524.92€.
-
KS = 25000 * (1 + 4 / 12 / 100)∧(12 * 5) = 30524.915
Damit sich die Verbindlichkeiten nach 5 Jahren auf 20000€ reduzieren müssen die 60 Monatsraten folgendem Zukunftswert entsprechen:
-
ZW = 30524.915 – 20000 = 10524.915
Formel (2) muss nun für die Ratenzahlung C aufgelöst werden und wir erhalten als Ergebnis:
-
C = 10524.915 * 4 / 12 / 100 / ((1 + 4 / 12 / 100)∧60 – 1) = 158.75
Beispiel 2: im vorhergehenden Abschnitt 2.1.1 hatten wir den Ratenkredit über 1000€ mit 36 Monatsraten von 29.08€ vollständig getilgt. Die aufgezinste Kreditsumme KS muss also hier dem Zukunftswert der Ratenzahlungen entsprechen.
-
KS = 1000 * (1 + 3 / 12 / 100)∧36 = 1094.05
ZW = 29.08 * ((1 + 3 / 12 / 100)∧36 – 1) / 3 * 12 * 100 = 1094.01
Die 4 Cents Differenz sind ein Rundungsfehler, weil die Raten zu 29.08€ auf volle Cents abgerundet wurden.
2.1.3 Sparplan
In einem Sparplan werden monatlich 100€ zu einem Zinssatz von 3% angelegt. Welche Summe wird innerhalb von 10 Jahren angespart? Lösung: der Zukunftswert der Sparraten kann über Formel (5) für vorschüssige Annuitäten berechnet werden.
-
ZWv = 100 * (1 + 3 / 12 / 100) * ((1 + 3 / 12 / 100)∧(10*12) – 1) / 3 * 12 * 100 = 14009.08
2.1.4 Rentenversicherung
Ein 35 jähriger Mann legt über 30 Jahre monatlich 100€ zu einem Jahreszins von 3% in einer privaten Rentenversicherung an. Die Versicherung rechnet bei Rentenbeginn mit einer Lebenserwartung des Mannes von weiteren 20 Jahren. Wie hoch ist die resultierende Monatsrente? Lösung: die Rente kann über vorschüssige Annuitäten nach Formel (5) für die Beitragsphase und Formel (4) für die Rentenphase ermittelt werden. Zunächst ist die Summe zu berechnen, welche nach 30 Jahren zur Finanzierung der Rente zur Verfügung stehen wird:
-
ZWv = 100 * (1 + 3 / 12 / 100) * ((1 + 3 / 12 / 100)∧(30*12)-1) / 3 * 12 * 100 = 58419.37
In der Rentenphase wird der nicht verbrauchte Betrag weiterhin zum Zinssatz von 3% verzinst. Der Gegenwartswert der Rentenzahlungen muss der zu Rentenbeginn angesparten Summe entsprechen. Die Monatsrente kann also errechnet werden, indem Formel (4) für die regelmäßige Zahlung C aufgelöst wird.
-
C = 58419.37 / (1 + 3 / 12 / 100) / (1 – (1 + 3 / 12 / 100)∧(-20*12)) * 3 / 12 / 100 = 323.18