Portfolios optimieren durch logarithmische Renditeberechnung

Die logarithmische Renditeberechnung ist eine einfache Methode zur Einpreisung von Risiken und Volatilität, die es Kleinanlegern ermöglicht, Portfolios zu optimieren. Die vorgeschlagene Technik bestimmt den Anteil einer risikobehafteten Position am Gesamtportfolio, der die Anlageperformance maximiert. Hierbei kann die Rendite durch Verkleinern einer gehebelten Position vom Negativen ins Positive wechseln. Gleichzeitig integriert die logarithmische Betrachtung der Auswirkungen von Kursrückgängen ein grundlegendes Risikomanagement in die Handelsstrategie.

Zur Einleitung wird erklärt, warum die meisten Anleger selbst bei überwiegend zutreffenden Kursprognosen mit hochvolatilen Positionen wie CFDs oder Futures Verluste machen. Es folgt die Beschreibung eines einfachen Verfahrens, riskante Positionen optimal im Gesamtportfolio zu gewichten. Der Artikel schließt mit einer Herleitung mathematischer Zusammenhänge, deren Verständnis für die Anwendung der Optimierungsmethode jedoch nicht zwingend erforderlich ist.

Warum machen die meisten Privatanleger Verluste mit CFDs und Futures?

Contracts for Differences (CFDs)^[2] und Futures sind Anlageinstrumente, deren Wert sich aus der Differenz des Einstands- und Ausstiegskurses ergibt. Je nach Hebelung resultieren hieraus starke Gewinne oder Verluste. In absoluten Prozenten gerechnet mögen sich diese im Regelfall ausgleichen. Folgt auf eine Transaktion mit 90 % Gewinn eine mit 90% Verlust, so klingt das vordergründig nach einem Nullsummenspiel. Nach einem Gewinn von 90 % genügt jedoch ein Verlust von 52,6 %, um zum Einstandswert zurückzugelangen. Auf einen Verlust von 90 % bedarf es zum Ausgleich hingegen eines Anstiegs von 900 %! Dieses Problem tritt allerdings erst in wiederholten Transaktionen zutage.

Ein praktisches Beispiel mit 70 % zutreffenden Prognosen

Angenommen es wäre möglich, mit einer Trefferwahrscheinlichkeit von 70 % steigende oder fallende Kurse vorherzusagen. Charttechniker werden zugestehen, dass dies selbst für Profis nicht leicht zu erreichen ist. Insbesondere, weil einiges für die gegenteilige Sicht nicht vorhersagbarer, zufälliger Kursschwankungen spricht, die unter Ökonomen verbreitet ist. Tatsächlich ähneln Finanzkurse eher Zufallspfaden, welche einer geometrischen Brownschen Molekularbewegung entsprechen^[3].

Als zweite Annahme sei, entsprechend der aktuellen Kursschwankungen am Markt, für ein gehebeltes Anlageinstrument entweder mit einer Wertsteigerung um 90 %, oder aber einer Wertminderung um 90 % zu rechnen.

Der Erwartungswert dieses Geschäfts, welcher dem durchschnittlichen Investitionserfolg entspricht, ist leicht zu ermitteln. Nach der Wahrscheinlichkeitstheorie ergibt sich dieser aus den beiden möglichen Endergebnissen, gewichtet mit ihren jeweiligen Wahrscheinlichkeiten. Steigt ein Einsatz von 100 € zu 70 % auf 190 €, und fällt er zu 30 % auf 10 €, so beträgt sein Erwartungs- bzw. Mittelwert 136 €, nämlich 0,7 mal 190 € plus 0,3 mal 10 €:

Mittelwert = 70% * 190 + 30% * 10
           = 133       + 3
           = 136
Gewinn     = (136 - 100) / 100 = 36%

Also ist dem Mittelwert entsprechend einen Gewinn von 36% zu erwarten. Diese Rechnung täuscht jedoch, weil sie Wiederanlageeffekte nicht einbezieht. In Abbildung 1 ist dieser Sachverhalt graphisch dargestellt. Tatsächlich werden 65,7 % der Anleger schon bei dreimaliger Wiederholung der Transaktion Verluste einfahren! Trotz einer fabelhaften Trefferquote von 70 % der Vorhersagen steigender oder fallender Kurse!

Szenarien der Wertentwicklung im Binomial-Baum

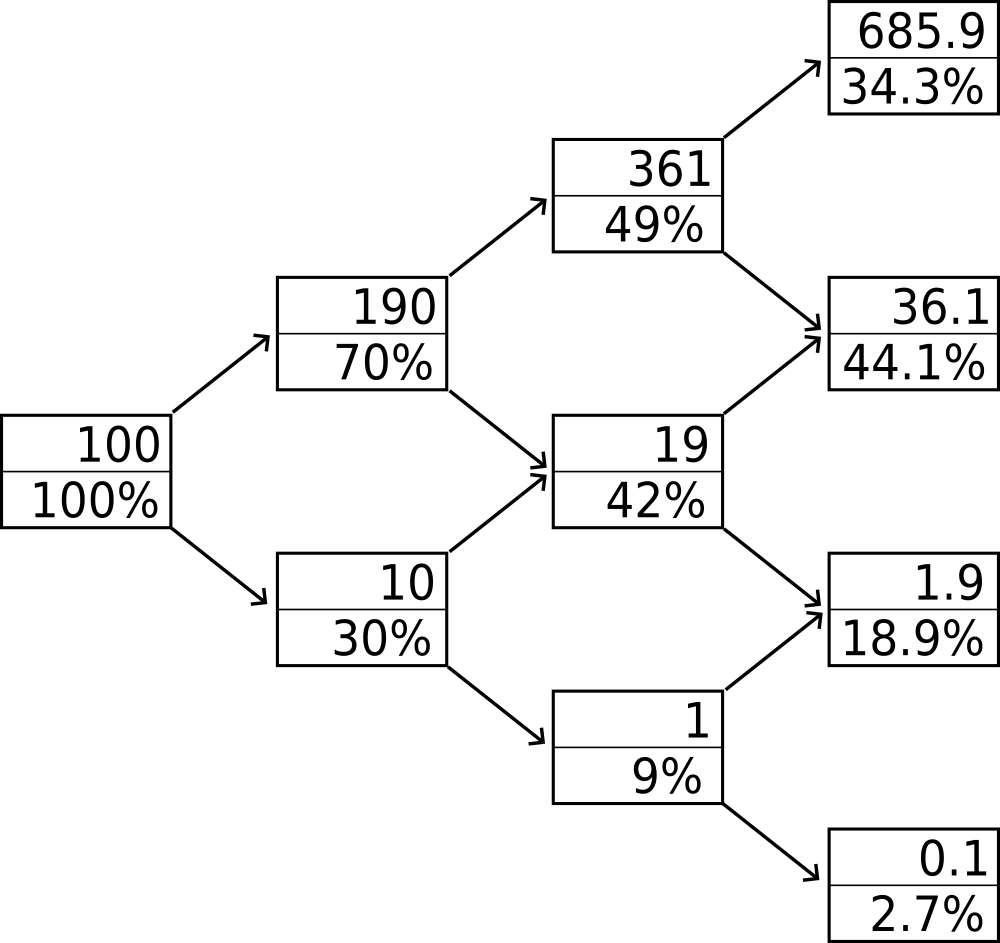
Mögliche Wertentwicklungen eines riskanten, durch Berechnung logarithmischer Renditen zu optimierenden Portfolios im Binomial-Baum. — Abbildung 1: Wertentwicklung bei dreimaliger Wiederholung einer Anlagestrategie mit ±90 % Gewinn bei 70 % Trefferquote. In den oberen Hälften der Knotenpunkte jeweils Portfoliowerte und in den unteren Eintrittswahrscheinlichkeiten in %.

Abbildung 1 zeigt einen sogenannten Binomial-Baum^[1] der möglichen Wertentwicklungen eines Einsatzes von 100 € bei dreimaliger Wiederholung einer Transaktion entsprechend des vorhergehenden Abschnitts, mit ±90 % Gewinn bei 70 % Trefferquote. Jeder Knotenpunkt enthält oben den Portfoliowert in Euro und unten die Wahrscheinlichkeit des Eintretens des entsprechenden Szenarios in %. Auf- und Abwärtspfeile zeigen 90 % Gewinn bzw. Verlust an.

Ganz links, an der Wurzel des Baums, steht der mit Sicherheit, also einer Wahrscheinlichkeit von 100 % verfügbare Einstandswert von 100 €. Im ersten Schritt finden sich die beiden schon diskutierten Ergebnisse von 190 € oder 10 €. Im zweiten Schritt gibt es drei Möglichkeiten von 361 €, 19 € und 1 €. Der dritte Schritt zeigt schließlich in den Knotenpunkten ganz rechts im Bild die vier möglichen Endergebnisse. Diese betragen 685,9 €, 36,1 €, sowie die praktischen Totalverluste von 1,9 € und 0,1 €. Nur im Knotenpunkt oben rechts machen Anleger Gewinne. Die Wahrscheinlichkeit von 34,3 %, den Knoten rechts oben zu erreichen, bedingt die bereits erwähnte Verlustwahrscheinlichkeit von 65,7 %. Diesen Wert erhält man auch durch Aufaddieren der Einzelwahrscheinlichkeiten der unteren drei Knoten auf der rechten Seite.

Verlustwahrscheinlichkeit = 44,1% + 18,9% + 2,7%
                          = 65,7%

Den vielen Verlierern stehen 34,3 % Gewinner mit phantastischen Wertsteigerungen von 585,9 % gegenüber. Die Realität des CFD-Investments sieht offensichtlich noch schlechter aus, glaubt man den offiziellen Warnungen vor gut 80 % an Anlegern, die Verluste erleiden. Kaum ein Investor kann schließlich Finanzkurse mit einer Trefferquote von 70 % vorhersagen.

Eine ausführliche Abhandlung der Mathematik von Binomial-Bäumen würde an dieser Stelle zu weit führen. Statt dessen können interessierte Leser das mitgelieferte Excel-Sheet studieren. Leider verfügt der Autor nur über eine englische Version von Libre-Office und deshalb sind internationalisierungsbedingte Inkompatibilitäten für deutsche Leser nicht auszuschließen.

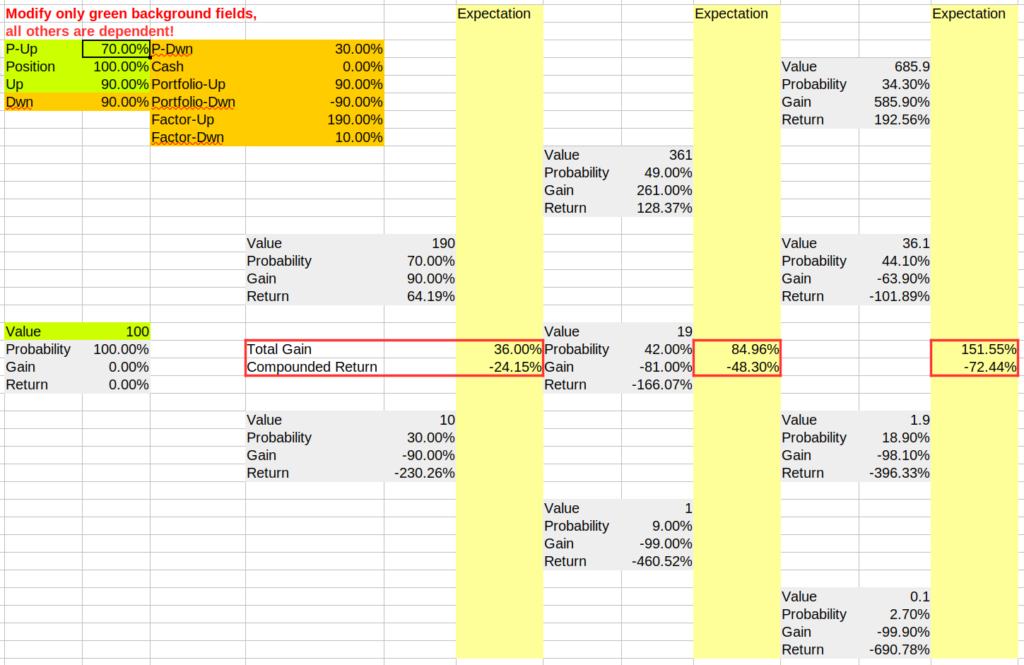
Screen-Shot eines Exel-Sheets zum Optimieren der Wertentwicklung eines Portfolios mit einer hochriskanten Position. — Abbildung 2: Screenshot der Portfolioanalyse in Excel. Neben den absoluten Gewinnen sind rot umrandet die logarithmischen Renditen enthalten.

Das Excel-Sheet öffnet sich durch klicken auf diesen Link.

Rendite riskanter Positionen richtig berechnen

Die vorangehenden Abschnitte zusammengefasst, bringt das besprochene Portfolio für die meisten Anleger nur Verluste, obwohl Einzeltransaktionen einen durchschnittlichen Gewinn von jeweils 36% versprechen. Offensichtlich ist der absolute Transaktionsgewinn kein geeignetes Maß zur Beurteilung von Anlagestrategien, weil Wiederanlageeffekte nicht berücksichtigt werden.

Zur Einführung eines besseren Ansatzes ist es zum Glück an dieser Stelle nicht nötig, den Zinseszinseffekt zu vertiefen. Vielmehr genügt es, sich an die Mathematik der gymnasialen Mittelstufe zu erinnern: Exponentialfunktion und Logarithmus.

Der erwartbare Erfolg riskanter Anlagestrategien kann auf einfache Weise mithilfe des natürlichen Logarithmus vorhergesagt werden. Steigt ein Portfolio vom Wert A auf den Wert B, erhält man folgendermaßen die logarithmische Rendite:

Logarithmische Rendite = ln(B/A)

Die erwartbare logarithmische Rendite E[r] des Geschäfts mit ±90 % Gewinn bei 70 % Trefferquote ist daher:

E[r] = 70% * ln(190/100) + 30% * ln(10/100)
     = 70% * 0,6419 + 30% * (-2,3026)
     = -24,15%

Dass also die Mehrheit der Anleger bei diesem Geschäft Verluste erleiden wird, drückt sich direkt im Erwartungswert E[r] der logarithmischen Rendite aus. Diese ist nämlich negativ mit -24,15 %. Die mathematischen Grundlagen des Gebrauchs logarithmischer Renditen sind im entsprechenden Abschnitt des Anhangs erläutert.

Riskante Portfolios optimieren

Die Rendite von Portfolios kann durch Verkleinerung des Anteils hochvolatiler Positionen vom Negativen ins Positive umschlagen. Für das im vorhergehenden diskutierte Geschäft mit ±90 % Gewinn bei 70 % korrekter Vorhersagen trifft dies zu. Hier steigt die Rendite von -24,15% auf ein Maximum +8,23%, wenn nur 44,4 % des Gesamtwerts investiert werden und die restlichen 56,6 % in Bar verbleiben. Weniger ist bisweilen mehr, oder anders gesagt wirken sich Strategien mit starker Hebelung oft nicht positiv auf den Gesamterfolg aus.

Eine Schwankungsbreite von ±90 % ist also zu hoch bei einer Wahrscheinlichkeit steigender Kurse von 70 %. Definiert man nun den Betrag der Schwankungsbreite als g und die Wahrscheinlichkeit steigender Kurse als P_u, so läßt sich die optimale Schwankungsbreite mittels folgender Formel berechnen:

\begin{aligned} g = &~P_u - \sqrt{P_u^2 - 2P_u + 1}\\ g = &~ 0~~ \forall~P_u \leq 0,5 \end{aligned}

Natürlich kann es nur Gewinne geben, wenn die Wahrscheinlichkeit steigender Kurse mehr als 50 % beträgt. Ansonsten ist das Maximum bei 100 % des Portfolios in Cash erreicht.

Für P_u = 70 % ergibt sich als optimale Schwankungsbreite:

g = 0,7 - sqrt(0,49 -1,4 + 1)
  = 0,7 - sqrt(0,09)
  = 0,7 - 0,3
  = 0,4 = 40%

Statt der ±90 % Schwankungsbreite des Beispiel-Portfolios wären also ±40 % optimal.

Hat man aber ein Finanz-Instrument mit festgelegter Schwankungsbreite g_i, so kann man den optimalen Anteil dieser Position am Gesamtportfolio aus der optimalen Schwankungsbreite g ermitteln. Es gilt für die Anteile der Cash-Position A_c und des Finanz-Instruments A_i:

\begin{aligned} A_i &= \frac{g}{g_i}\\ A_c &= 1 - A_i \end{aligned}

Hätten wir also angewandt aufs Beispiel ein Finanz-Instrument mit einer Schwankungsbreite g_i von ±90 %, und wollten daraus ein Portfolio mit optimaler Schwankungsbreite g von ±40 % erstellen, so ergibt sich für A_i:

A_i = 40% / 90% = 44,44%

Dies ist der bereits angesprochene Anteil von 44,4 % der riskanten Position, welcher das Portfolio optimiert.

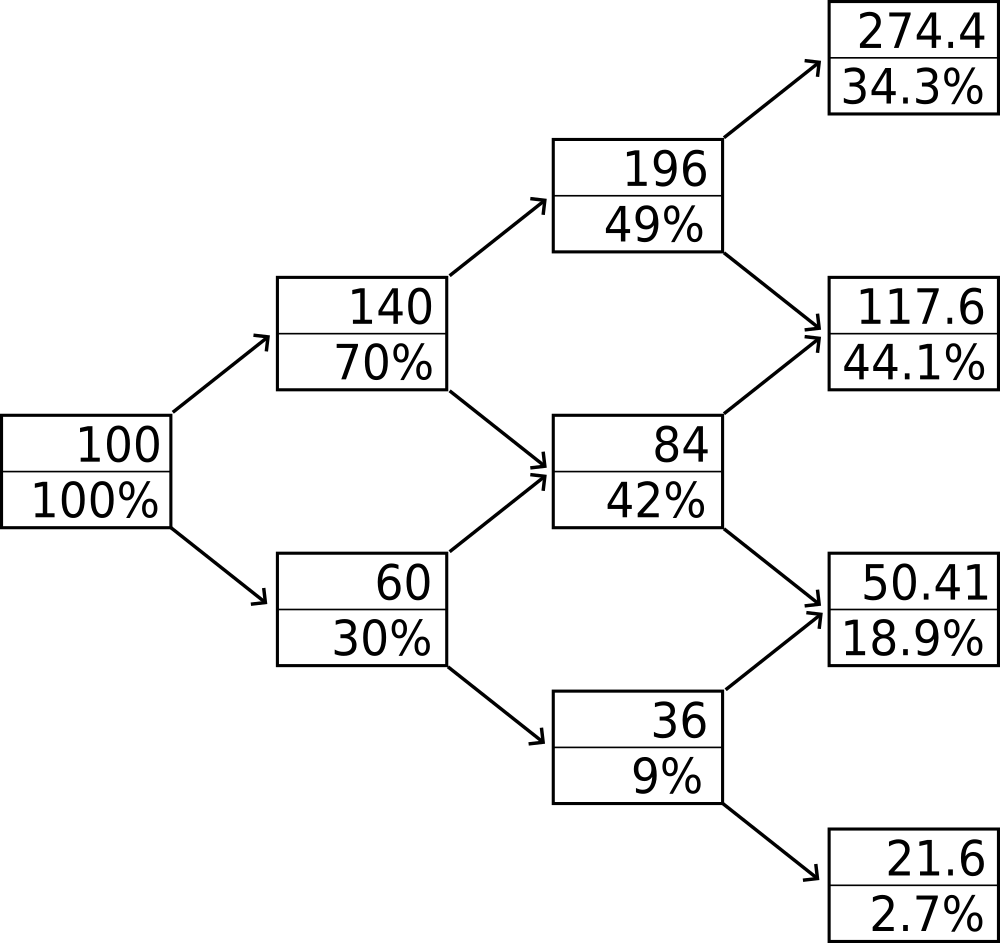
Optimiertes Portfolio als Binomial-Baum. — Abbildung 3: Optimiertes Portfolio mit 40 % Schwankungsbreite im Binomial-Baum.

Zum Schluss noch in Abbildung 3 das optimierte Portfolio mit 40 % Schwankungsbreite im Binomial-Baum. Zwar ist der Wertzuwachs im Knoten rechts oben mit 174,4 % deutlich geringer als zuvor. Dafür erwirtschaften nun aber insgesamt 78,4 % der Anleger Gewinne!

Mathematische Grundlagen

Im Abschnitt zur Rendite riskanter Positionen wurde postuliert, zur Risiko- und Erfolgsabschätzung eigne sich am besten der natürliche Logarithmus. Dies wird nun begründet. Danach folgt die Herleitung der Formel zur optimalen Schwankungsbreite.

Warum den natürlichen Logarithmus zur Renditeberechnung?

Der natürliche Logarithmus bemisst die Geschwindigkeit exponentiellen Wachstums, was der idealen Wertentwicklung von Anlageportfolios entspricht. Diese besteht in der regelmäßigen Erwirtschaftung von Gewinnen, deren Wiederanlage auf lange Sicht den Gesamtwert dominiert. Der resultierende exponentielle Verlauf ist bei festverzinslichen Anlagen als Zinseszinseffekt bekannt. Je kürzer dabei die Perioden zur Wiederanlage, desto mehr nähert sich der Zinseszins einer Exponentialfunktion zur Basis der Eulerschen Zahl e an^[4]. Der Wert eines Portfolios B in Abhängigkeit der Zeit t (in Jahren) kann deswegen als Exponentialfunktion mit der Wachstumsrate bzw. langfristigen Rendite r beschrieben werden:

B(t) = B(0) \cdot exp(r \cdot t)

Die Exponentialfunktion hat folgende sehr nützliche Eigenheit:

\begin{aligned} exp(x) \cdot exp(y) = exp(x+y) \end{aligned}

Für die Umkehrfunktion, den Logarithmus, gilt:

ln(X \cdot Y) = ln(X) + ln(Y)

Also ergänzen Exponentialfunktion und Logarithmus einander in der Überführung von Summen in Produkte. Wächst nun ein Portfolio in zwei Zeitschritten um die Faktoren X und Y, so ergeben sich die Werte x und y, welche sich im Argument der Exponentialfunktion einfach aufaddieren lassen, aus dem Ziehen des Logarithmus:

\begin{aligned} x := ln(X)\\ y := ln(Y) \end{aligned}

Allgemeiner gesagt kann die Wertentwicklung B eines Portfolios als das Produkt einer langen Kette aufeinanderfolgender Finanztransaktionen F verstanden werden. Mit einem Einstandswert von B₀ ist dann der Portfoliowert B_n nach n Transaktionen:

B_n = B_0\prod_{i=1}^{n}F_i

Jeder Faktor F_i ist dabei ein Ausdruck der Rendite von Einzeltransaktionen. Diese Rendite kann sowohl in absoluten Gewinnen, als auch logarithmisch angegeben werden.

\begin{aligned} F_i &= \frac{B_i}{B_{i-1}} = 1 + G_i\\ F_i &= exp(ln(\frac{B_i}{B_{i-1}})) = exp(f_i) \end{aligned}

Angewandt auf die Kette von n Transaktionen bedeutet dies:

B_n = B_0~exp(ln(\prod_{i=1}^{n}F_i))

Im Gegensatz zu den absoluten Gewinnen G_i sind es jedoch die logarithmischen Renditen f_i, welche sich im Sinne der Wertentwicklung tatsächlich aufsummieren:

B_n = B_0~exp(\sum_{i=1}^{n}f_i)

Das Portfolio erfährt genau dann eine Wertsteigerung, wenn der Mittelwert der logarithmischen Renditen f_i über Null liegt:

\begin{aligned} \bar{f} &= \frac{1}{n} \sum_{i=1}^{n}f_i\\ \bar{f} &> 0~~\mathrm{für~Gewinne} \end{aligned}

Zur Portfolio-Optimierung und einer besseren Einschätzung von Risiken genügt es, die logarithmischen Renditen unabhängig von den Zeitspannen der Einzeltransaktionen zu betrachten. In Logarithmen ist jedoch auch die Performance leicht zu ermitteln. Für die langfristige Rendite r dividiert man einfach die Summe der transaktionsbezogenen Renditen f_i durch die Gesamtzeit t:

r = \frac{1}{t} \sum_{i=1}^{n}f_i

Herleitung optimaler Schwankungsbreiten

Zur Optimierung von Portfolios lassen sich bei bekannter Wahrscheinlichkeit steigender Kurse die Schwankungsbreiten für maximale Renditen berechnen. Mit g als dem Betrag der Schwankungsbreite und P_u als Wahrscheinlichkeit steigender Kurse gilt für die Rendite r:

\begin{aligned} r &= ln(1+g)P_u\\ &~+ ln(1-g)(1-P_u) \end{aligned}

Im Punkt der optimalen Schwankungsbreite muss die erste Ableitung der Rendite Null sein.

\begin{aligned} \frac{\partial r}{\partial g} = 0 \end{aligned}

Mit ln(x)‘ = 1/x und der Kettenregel ergibt sich als erste Ableitung:

\begin{aligned} \frac{\partial r}{\partial g} &= P_u \frac{1}{1+g}\\ &~+ (1-P_u)(-1) \frac{1}{1-g} \end{aligned}

Nach einigen Umformungen erhält man:

\begin{aligned} g^2 -2P_u~g +2 P_u -1 = 0 \end{aligned}

Für quadratische Gleichungen gibt es folgende allgemeine Lösungsformel:

\begin{aligned} &a g^2 + bg + c = 0\\ &g_{1,2} = \frac{-b~\pm \sqrt{b^2 - 4ac}}{2a} \end{aligned}

Durch Einsetzen der Koeffizienten bekommt man:

g_{1,2} = P_u~\pm \sqrt{P_u^2 - 2P_u + 1}

Die maximale Rendite fällt auf den kleineren der Werte:

g = P_u - \sqrt{P_u^2 - 2P_u + 1}

Monte-Carlo-Simulation von Renditen

Wesentlich aussagekräftigere Ergebnisse als unter den vereinfachenden Modellvorstellungen dieses Artikel lassen sich mithilfe einer Monte-Carlo-Simulation von Renditen^[5] erzielen. Diese bildet alle möglichen Szenarien der Wertentwicklung ab und erfasst auch verhältnismäßig unwahrscheinliche Ergebnisse mit Totalverlust.

Die im Rahmen des Artikels hergeleiteten optimalen Schwankungsbreiten verstehen sich als Obergrenzen riskanter Positionen. Niemand kann bei risikobehafteten Finanztransaktionen Gewinne garantieren und der Autor übernimmt diesbezüglich keinerlei Haftung.