Dieser Zinsrechner ermittelt die Ratenzahlung zur Tilgung eines Ratenkredits. Die Berechnung gilt für Kredite, bei denen Zinssatz und Raten über die Vertragslaufdauer gleich bleiben. Beispiele für diesen Vertragstyp sind Hypotheken und Verbraucherkredite. Eine Bedienungsanleitung sowie Erläuterungen zu Tilgung und Kosten von Ratenkrediten folgen auf das Berechnungsformular.
Bedienungsanleitung zur Berechnung der Ratenzahlung zum Ratenkredit
Bitte füllen Sie das Formular mit der Höhe des an Sie ausgezahlten Kredits, den am Ende der Laufzeit noch ausstehenden beziehungsweise nicht getilgten Kreditbetrag, dem Kreditzinssatz und der Kreditlaufzeit. Alle Felder oberhalb des Berechnen-Buttons sind Eingabewerte, die Sie nach Bedarf ändern können. Aus diesen Angaben ermittelt der Finanzrechner die Höhe der regelmäßig zu zahlenden Raten.
Die Laufzeit des Kredits beziehungsweise Darlehens entspricht dem Zeitraum in Jahren, der Ihnen zur Rückzahlung zusteht.
Standardmäßig setzt das Formular zwölf Jahresraten beziehungsweise monatliche Raten ein. Dies entspricht den üblichen Konditionen von Hypotheken und Verbraucherkrediten und dürfte für den meisten Anwender zutreffend sein. Sie können dies jedoch auf vier (vierteljährliche Raten), zwei (halbjährliche Raten) oder eins (jährliche Raten) überschreiben.
Zusätzlich zur Ratenzahlung gibt der Rechner im Detailbereich Zwischensalden aus. Da diese Liste ziemlich lang werden kann, können Sie sie ausblenden, indem Sie auf das Label „verbergen -“ in der rechten oberen Ecke klicken.
Tilgung von Ratenkrediten
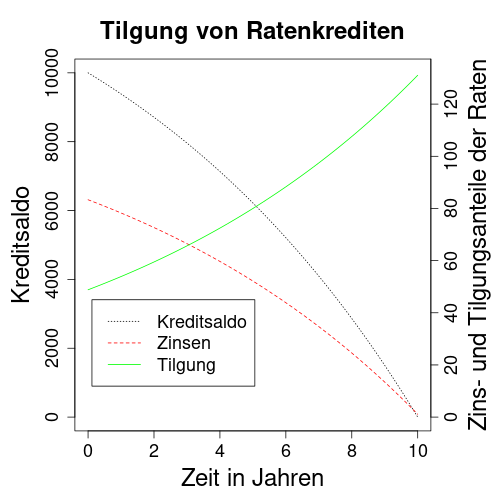
Die obige Grafik zeigt Tilgungs- und Zinsanteile von Ratenzahlungen eines Musterkreditvertrags. Wegen der unterschiedlichen Größenordnung von Saldo und Raten haben die linke und rechte Achse verschiedene Skalierungen. Die rot gestrichelten Zinszahlungen und grünen Tilgungsanteils bemessen sich an der rechten Achse. Die gepunktete schwarze Linie in Skalierung der linken Achse ist der ausstehende Kreditsaldo. Da die Raten konstant sind, summieren sich deren Zins- und Tilgungsanteile immer auf den gleichen Betrag. Mit sinkendem Kreditsaldo steigen jedoch die Tilgungsanteile, während sich die Zinszahlungen verringern. In der Grafik sieht man dies an der nach unten gekrümmten Zinslinie beziehungsweise der nach oben gekrümmten Tilgungslinie.
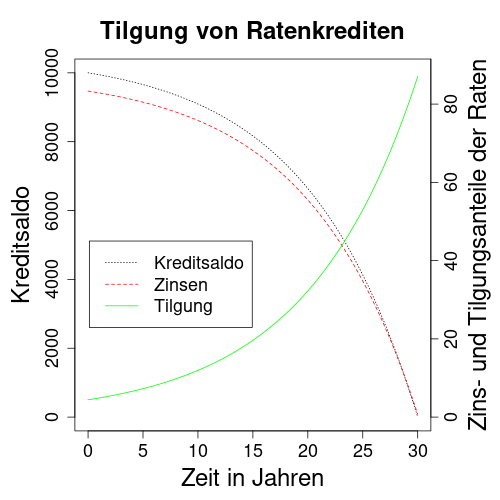
Im zweiten Bild ist ein Ratenkredit wie im ersten Beispiel zu sehen, jedoch mit 30 Jahren Laufdauer. Weil mehr Zeit zur Rückzahlung bleibt, verringern sich die Raten von 132,15 € auf 87,76 €. Während jedoch bei 10 Jahren Laufdauer die erste Rate noch einen Tilgungsanteil von 48,82 € hatte, verringert sich dieser bei 30 Jahren Laufdauer auf nur 4,42 €. Zwar sind bei längerer Laufdauer die Raten niedriger, dafür aber die Zinszahlungen in Summe deutlich höher. Sie steigen von 5.858,00 € bei 10 Jahren auf 21.593,60 € bei 30 Jahren Laufdauer.
Kurz gesagt, je mehr Zeit Sie sich nehmen, einen Kredit zurückzuzahlen, desto teurer wird es.
Mathematische Formel für die Raten eines Ratenkredits
Die Berechnung zur Ratenzahlung eines Ratenkredits verwendet folgende Formel:
Rate = r / m / ((1 + r/m)(m*t) - 1)
* (L0 * (1 + r/m)(m*t) - L1)
Rate: Betrag der regelmäßigen Raten
r: Zinssatz
m: Anzahl der Raten pro Jahr
t: Laufdauer des Kredits in Jahren
L0: Kreditsaldo zum Vertragsbeginn (t=0)
L1: Offener Kreditsaldo bei VertragsendeReferenzen
Ratenkredite: Wikipedia.org
Ähnliche Berechnungen
Ratenzahlung zum Ratenkredit auf Englisch: finalgebra.com