Dieser Finanzrechner ermittelt den Zinssatz zu Ratenkrediten, der zu den übrigen Konditionen, also Laufdauer, Kreditsalden und Raten passt. Er ist anwendbar für Vertragstypen mit festem Zins und konstanten Raten, wie Hypotheken, Autokredite und andere Verbraucherkredite. Eine Bedienungsanleitung sowie Erläuterungen zum Einfluss der Raten auf den zugrunde liegenden Zinssatz folgen auf das Berechnungsformular.
Bedienungsanleitung zur Berechnung des Zinssatzes von Ratenkrediten
Bitte füllen Sie das Formular mit dem ausgezahlten Kreditbetrag, den am Ende der Laufdauer noch offenen beziehungsweise nicht getilgten Kreditbetrag, den Ratenzahlungen sowie der Laufzeit in Jahren. Alle Felder oberhalb des Berechnen-Buttons sind Eingabewerte, die Sie nach Bedarf ändern können. Aus diesen Angaben ermittelt der Finanzrechner den zugrunde liegenden Zinssatz, also den Zinssatz, der zu den übrigen Konditionen passt.
Die Laufzeit des Kredits entspricht dem Zeitraum in Jahren, der Ihnen zur Rückzahlung zusteht.
Standardmäßig setzt das Formular zwölf Jahresraten beziehungsweise monatliche Raten ein. Dies entspricht den üblichen Konditionen von Hypotheken und Verbraucherkrediten und dürfte für den meisten Anwender zutreffend sein. Sie können dies jedoch auf vier (vierteljährliche Raten), zwei (halbjährliche Raten) oder eins (jährliche Raten) überschreiben.
Zusätzlich zum Kreditsaldo am Ende der Laufzeit gibt der Rechner im Detailbereich Zwischensalden aus. Da diese Liste ziemlich lang werden kann, können Sie sie ausblenden, indem Sie auf das Label „verbergen -“ in der rechten oberen Ecke klicken.
Der Kreditzins in Abhängigkeit der Raten
Dieser Abschnitt erläutert die Abhängigkeit zwischen Ratenhöhe und zugrunde liegendem Zinssatz. In der Regel steigt bei festgelegtem Anfangs- und Endkreditsaldo sowie festgelegter Vertragslaufzeit der zugrunde liegende Zinssatz mit der Höhe der Raten.
Dabei gibt es für jede Kombination aus Kreditsalden und Ratenhöhe bis zu einen zugrunde liegenden Zinssatz, welcher die Werte in Einklang bringt. Wenn also die gewählten Konditionen Sinn ergeben und zu einem Kreditvertrag passen, kann der Rechner eine Lösung finden. Andernfalls gibt er die Meldung „Fehler in Berechnungsschleife“ aus. Ein Beispiel für solch eine Wertekombination, die keinen sinnvollen Kreditvertrag ergeben kann, wäre eine positive ausgezahlte Kreditsumme, welche mit negativen Raten vollständig getilgt werden soll.
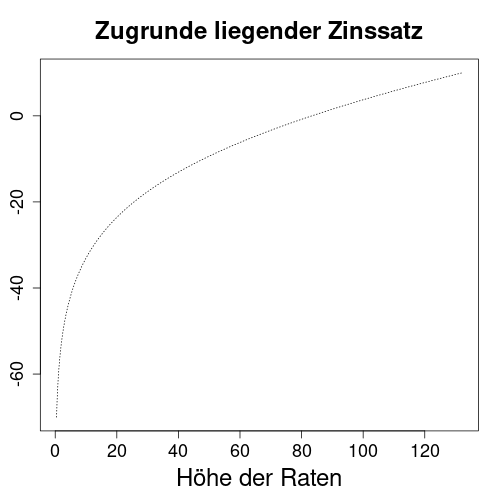
Die obige Grafik zeigt Beispiele für unrealistische Kreditvergabeszenarien, die dennoch den Zahlen nach stimmige Kreditverträge ergeben können. Das Diagramm hat Zinssätze auf seiner vertikalen Achse und monatliche Raten auf seiner horizontalen Achse. Die gepunktete Linie zeigt also die zugrunde liegenden Zinssätze für verschiedene Höhen der monatlichen Raten. Alle Szenarien gehen von einem Darlehen in Höhe von 10.000 € aus, welches über einen Zeitraum von 10 Jahren vollständig zurückzuzahlen ist. Wenn wir zum Beispiel einen Kreditgeber finden könnten, der -70 % Zinsen verlangt, dann würden Raten von weniger als 1€ monatlich ausreichen, um den Kredit abzulösen. Denn bei Negativzinsen bezahlt der Kreditgeber den Kreditnehmer dafür, dass er Geld bekommt.
Geht man jedoch von realistischen Kreditszenarien aus, beispielsweise mit monatlichen Raten von 110 €, dann findet der Rechner einen vernünftigen Zinssatz von rund 5,8 % als Lösung.
Mathematische Formel
Der Rechner verwendet folgende Formel für den zugrunde liegenden Zinssatz zu Ratenkrediten:
I(r) = r / m / ((1 + r/m)(m*t) - 1)
* (L0 * (1 + r/m)(m*t) - L1)
argminr { Inst - I(r) }
Inst: Ratenhöhe
I(r): Ratenhöhe als Funktion des Zinssatzes r
r: Zinssatz
m: Anzahl jährlicher Raten
t: Laufdauer des Vertrages in Jahren
L0: bei Vertragsbeginn ausgezahlte Kreditsumme
L1: bei Vertragsende noch ungetilgte KreditsummeDa der Zinssatz r in mehreren Potenzen in die Formeln für Ratenkredite eingeht, gibt es keine einfache analytische Lösung. Allerdings können wir die Formel für die Ratenhöhe bei gegebenem Zinssatz und Darlehenssummen wiederverwenden. Der Rechner sucht dann nach einem Zinssatz r, für den die Ratenhöhe nahe einem gewünschten Zielwert liegt. Dies wird mathematisch mit argminr umschrieben. In der konkreten Umsetzung setzt die Berechnungsschleife Probewerte für den Zinssatz r ein, um die Differenz zwischen der Zielrate Inst und I(r) zu minimieren.
Mit einem geeigneten Suchalgorithmus findet die Berechnung hochpräzise Lösungen in weniger als 10 Iterationen.
Referenzen
Tilgungsplan zu Ratenkrediten: Wikipedia.org
Ähnliche Berechnungen
Ratenzahlung zu Ratenkredit: zinseszins.de
Zinssatz zu Ratenkredit auf Englisch: finalgebra.com