Geometrische Brownsche Molekularbewegung

Die geometrische Brownsche Molekularbewegung (GBM) ist eine Art Random-Walk-Modell, welches Fluktuationen ähnlich derer von Aktiencharts erzeugt. Dabei beschreibt der zugrunde liegende Datengenerierungsprozess (DGP) exponentielles Wachstum, das durch normalverteilte Zufallsschocks abgelenkt wird.

Der Wert eines GBM-Prozesses S_t ändert sich wie in der nachfolgenden stochastischen Differentialgleichung (SDE) definiert:

\begin{align}
dS_t = r S_t dt + \sigma S_t dW_t
\end{align}

\begin{aligned}
S_t &: \mathrm{Wert~zum~Zeitpunkt}~t\\
r &: \mathrm{Wachstumsrate}\\
\sigma &: \mathrm{Volatilität}\\
W_t &: \mathrm{Wiener~Prozess}
\end{aligned}

In Gleichung (1) treibt der deterministische Term rS_tdt das exponentielle Wachstum und der stochastische Term σS_t​dW_t​ steuert zufällige Schocks bei. Innerhalb des stochastischen Terms ist es der Wiener-Prozess^[4] W_t, welcher die zufällige Variabilität verursacht. Wiener-Prozesse integrieren Gaußsches weißes Rauschen und haben die folgenden grundlegenden Eigenschaften:

\begin{align}
&W_0 = 0\\
&W_{t}  \sim~N(0,t)
\end{align}

Als zusätzliche Eigenschaft von weißem Rauschen sind nicht überlappende Inkremente von W_t unabhängig.

Die SDE aus (1) integriert sich in Itô-Calculus^[1] zu folgender analytischen Lösung:

\begin{align}
S_t = S_0~e^{(r - \frac{\sigma^2}{2})t + \sigma W_t}
\end{align}

Da E[W_t] null ist, entspricht jedoch der Erwartungswert von GBM-Pfaden einem nicht von zufälligen Schocks beeinflussten geometrischem Wachstum:

\begin{aligned}
E[S_t] = S_0 ~ e^{rt}
\end{aligned}

GBM in diskreten Zeitschritten

Simulationen und andere praktische Anwendungen der GBM verwenden eine Version von Gleichung (1) in diskreten Zeitschritten. Aufgrund der Distribution aus (3) haben die Inkremente dW_t über die Zeitspanne Δt eine Varianz von Δt. Daher kann das aggregierte Inkrement ΔW_t ausgedrückt werden als:

\begin{aligned}
\Delta W_t = \sqrt{\Delta t} ~ \epsilon_t\\
\epsilon_t \overset{\mathrm{iid}}{\sim} N(0,1)
\end{aligned}

Folglich ist die diskrete Version von Gleichung (1) gegeben durch:

\begin{align}
\Delta S_t &= r S_t \Delta t + \sigma S_t \sqrt{\Delta t} ~\epsilon_t
\end{align}

In der Computerstatistik werden die unabhängig und identisch verteilten (iid) Schocks ϵ_t einfach aus einer Standardnormalverteilung gezogen. Es ist daher einfach, GBM-Pfade ausgehend von einem Anfangswert S_t und rekursiven Anwendungen von Gleichung (5) zu erhalten.

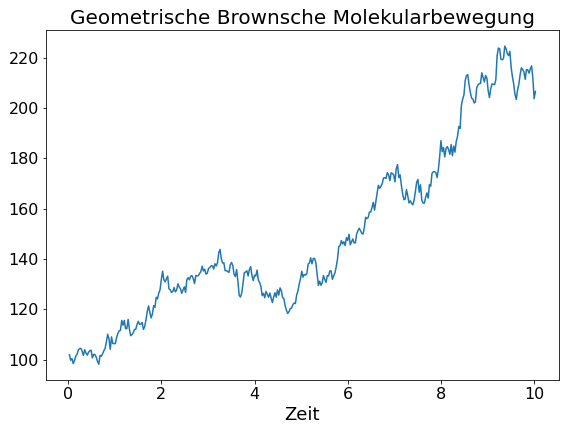
Abbildung 1 zeigt ein Beispiel für einen geometrischen Brownschen Bewegungspfad mit einem Startwert von 100, 4 % jährlichem Wachstum und 10 % Volatilität entwickelt über einen Zeitraum von 10 Jahren. Aufgrund der Ähnlichkeit der geometrischen Brownschen Bewegung mit Börsenkursen nutzen Ökonomen zur Preisfindung von Derivaten mitunter Projektionen aus solchen Zufallspfaden.

Mathematische Herleitung der GBM Rendite mittels Itô Calculus

Um die Investitionsrendite zu erhalten, schreibt man den GBM-Prozess aus Gleichung (1) in Logarithmen um. Dazu ist Itô-Calculus^[1] erforderlich, welcher Infinitesimale als Taylor-Reihenentwicklungen zweiter Ordnung nähert:

d(f(x)) = \frac{\partial{f(x)}}{\partial{x}}dx + \frac{\partial^2{f(x)}}{2~\partial{x}}dx^2

Für die logarithmische Rendite setzt man nun f(x)=ln(x):

\begin{aligned}
\frac{\partial ln(S_t)}{\partial S_t} &= \frac{1}{S_t}\\
d(ln(S_t)) &= \frac{dS_t}{S_t} - \frac{1}{2}\frac{dS_t^2}{S_t^2}\\
\end{aligned}

Hierbei ist der Term dS_t² das Quadrat der SDE (1):

\begin{aligned}
dS_t^2 = &~dS_t \cdot dS_t\\
dS_t^2 = &~r^2 S_t^2 dt^2\\
&+ 2~r\sigma~dt~dW_t\\
&+ \sigma^2 S_t^2 dW_t^2
\end{aligned}

In Infinitesimalrechnung nähert sich dt² schneller gegen Null als dt→0. Dies gilt in ähnlicher Weise für das Produkt dt⋅dW_t. Dahingegen ist der Erwartungswert von dW_t² proportional zu dt, weil ja die Varianz von W_t den Wert t hat. Deshalb ist der dW_t² der einzige Term von dS_t² mit einem Einfluss auf das Endergebnis in Form einer deterministischen Drift der Größenordnung O(t). Durch Substitution in die Taylor-Reihe ergibt sich:

\begin{aligned}
d(ln(S_t)) &= \frac{dS_t}{S_t} - \frac{1}{2}\frac{dS_t^2}{S_t^2}\\
d~lnS_t &= \frac{dS_t}{S_t} - \frac{1}{2}\sigma^2dt
\end{aligned}

Die logarithmische Variante der GBM-Prozessgleichung ist damit:

\begin{align}
d~lnS_t &= (r - \frac{\sigma^2}{2})dt + \sigma dW_t
\end{align}

Die Renditen der GBM-Pfade werden also um einen Volatilitätsterm σ²/2 geschmälert. Weil E[σdW_t] Null ist, ergibt sich als Erwartungswert μ der Rendite:

\begin{align}
\mu = r - \frac{\sigma^2}{2}
\end{align}

Weiterhin lässt sich SDE (1) nun lösen, indem man zuerst Gleichung (6) über die Zeit integriert:

\begin{aligned}
ln(S_t) &= \int (r - \frac{\sigma^2}{2})dt + \sigma dW_t\\
ln (S_t) &= (r - \frac{\sigma^2}{2})t + \sigma W_t
\end{aligned}

In Gleichung (4), der Lösung zu SDE (1), wird nur noch die Exponentialfunktion auf obenstehendes Ergebnis angewandt und als Anfangsbedingung S_t(0)=S₀ gesetzt.

Herleitung der GBM-Varianz

Abschließend eine kurze Herleitung der GBM-Varianz. Die Varianz einer Zufallsvariablen ergibt sich grundsätzlich aus ihren ersten beiden Momenten:

\begin{align}
Var[X] &=E[X^2] - E[X]^2
\end{align}

Aus den Gleichungen (6) und (7) ergibt sich eine normalverteilte Rendite von GBM-Pfaden mit Erwartungswert μ und Varianz σ²:

\begin{align}
d~ln(S_t) \sim N(\mu, \sigma^2)
\end{align}

Per Definition ist eine Zufallsvariable lognormal verteilt, wenn ihr Logarithmus normalverteilt ist. Nun wird die lognormal verteilte Zufallsvariable X definiert als:

X = e^{d~ln(S_t)}

Die Momente E[X] und E[X²] können der momentenerzeugenden Funktion für lognormale Variablen entnommen werden^[3]:

E[X^n] = exp(n\mu + \frac{n^2\sigma^2}{2})

Für das erste und zweite Moment bekommt man also:

\begin{align}
E[X] &= e^{\mu + \frac{\sigma^2}{2}}\\
E[X^2] &= e^{2 \mu + 2 \sigma^2}
\end{align}

Gleichungen (10) und (11) eingesetzt in (8) ergeben:

\begin{align}
Var[X] = e^{2\mu + \sigma^2}(e^{\sigma^2}-1)
\end{align}

Entsprechend der Definition momenterzeugender Funktionen^[2] gilt das Ergebnis aus Gleichung (12) für eine lognormal verteilte Zufallsvariable mit dem Einheitswert Eins zum Zeitpunkt Null. Für einen GBM-Pfad, der zum Zeitpunkt Null mit einem Wert S₀ beginnt, also die Infinitesimale aus Gleichung (9) aufintegriert, sind dann die Momente:

\begin{aligned}
E[S_t] &= S_0~e^{(\mu + \frac{\sigma^2}{2})~t}\\
E[S_t^2] &= S_0^2~e^{(2 \mu + 2 \sigma^2)~t}
\end{aligned}

Nun substituiert man r = μ + σ²/2 zurück, um zu den Endergebnissen des Erwartungswerts und der Varianz von GBM-Pfaden zu gelangen:

\begin{aligned}
E[S_t]&=S_0e^{r t}\\
Var[S_t]&=S_0^2e^{2r t}(e^{\sigma^2 t} -1)
\end{aligned}

Referenzen

[1] Itô calculus: Wikipedia.org

[2] Moment Generating Functions: Statlect.com

[3] Moments of Lognormal Distribution: Statlect.com

[4] Wiener Process: Wikipedia.org

Verwandte Themen

Geometrische Brownsche Molekularbewegung auf Englisch: finalgebra.com